Latest news about Bitcoin and all cryptocurrencies. Your daily crypto news habit.
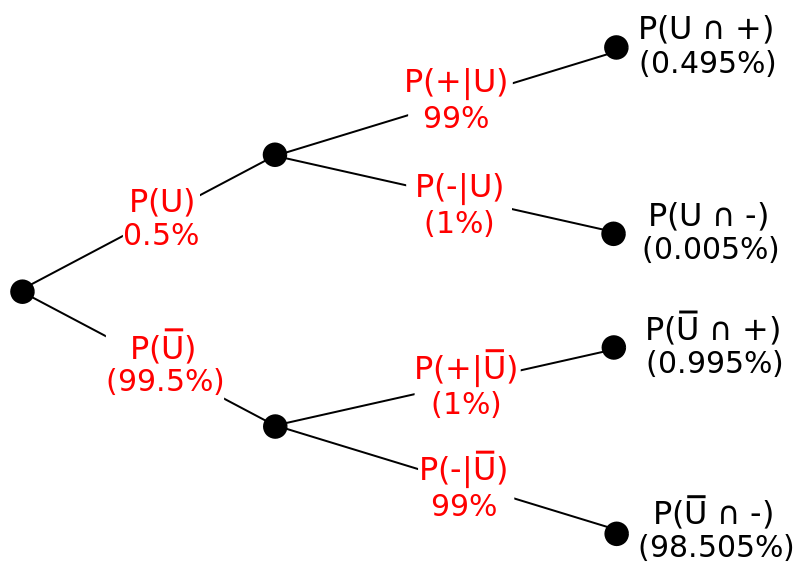 source : https://en.wikipedia.org/wiki/Bayes%27_theorem#/media/File:Bayes_theorem_drugs_example_tree.svg
source : https://en.wikipedia.org/wiki/Bayes%27_theorem#/media/File:Bayes_theorem_drugs_example_tree.svg
Hi Folks !! In this post i will discuss about the tricks and tips that i use to solve questions based on probability and i will also discuss about where the concept of probability is used in Statistics and ML.
Note: [ This post is on probability and probability only and not on ML Algorithms that uses probability. But I assure you, after reading this post you will feel confident in reading and understanding all the Probability based ML -Algo’s like — {Naive Bayes | Bayesian Statistics etc .. } or in Stats like — {Binomial Probability Distribution etc ]. So without wasting time, lets get started .
Basics
Formula => P(Event) = Favourable Outcomes / Total Possible Outcomes . Lets look at some examples:
- Problem: Throwing a Dice (1 time ) — Means [1,2,3,4,5,6] ie. total possible outcomes = 6. What is the probability of getting 5 on throwing a dice ? Ans : 1 / 6 .
- Problem: Tossing a Coin (1 time) — Means [Heads , Tails ] ie. Total possible outcomes = 2. What is the probability of getting a Head or Tail on tossing a coin? Ans: p(H)= 1/2 , p(T) =1/2
- Problem: Bucket with different colour balls and you are selecting a particular colour ball — Means total possible outcomes = number of balls in bucket . A bucket contains 10 green balls 7 blue balls and 3 white balls. You pick up a ball from basket (1 time) . What is the probability of getting a green ball ? Ans : 10 / (10 + 7 + 3) = 0.5
Now lets make this thing a little interesting !!!
What if i say, Throw 1 dice 10 times and find the probability of getting number ‘5’ exactly 7 times . Or Throw 5 dice together and find the probability of getting a sum 25 ?? [ Answer it in the comments section :) ] Tough huh !! Not really … To answer these questions you need to know few concepts . Lets look at them closely —
Types of Events
Mutually Exclusive events
- Two events are mutually exclusive if they do not occur at same time .
- Example : Head or Tail cannot occur at same time on tossing a coin.
- Question: Two dice are rolled what is the probability that the sum of numbers rolled is either 5 or 9 ? Ans : P(AUB) = P(A) + P(B)
Independent Events
- Two events are independent when the result of one event does not affect the other . They both are pure independent events .
- Example: Tossing a coin 2 times one after the other are independent events .
- Question: two dice are thrown one after the other . what is a probability of getting an even on both dice ? Ans : P(A)*P(B) = 3/6*3/6
Dependent Events
- If the result of one event affects the result of other then both events are dependent.
- Example: A basket has 10 balls (5 Blue and 5 White) and you select the first ball and keep it aside and then you select another ball from the basket .
- Now, lets make a question out of point 2 . what is the P of getting blue both times ? Ans: P(A) * P(B,once A occurred ) = 5/10*4/9
- P(AUB) = P(A)*P(B, once A has occurred)
Conditional Probability
- This is based on the concept of dependent events , where probability that an event A takes place will depend on another event B.
- Conditional Probability of an Event B given A [represented by=> P(B/A)]
- Formula => P(B/A) = P(A and B intersection) / P(A)
- Example: Suppose, I wrote 2 post about “probability” on Hackernoon and found that 25% of viewers read both of my post and 42% of viewers read only my 1st post .Now, What percent of those viewers who read my 1st post also read my 2nd post? ANS : .25/.42 = P(1st intersection 2nd) / P(1st) = 60% = P(2nd/1st) ( I hope you got this one ).
Bayes Theorem
- It describes the probability of an event, based on prior knowledge of conditions that might be related to the event.
- Formula : P(A/B) = P(B/A).P(A)/P(B)
Bayes theorem and Conditional Probability question style are very much inter-related. What i mean is that you can easily convert a Bayes theorem question to a one on Conditional probability and Vice versa by just changing 1 line of the entire question . Lets Look an Example :
Q. There are 2 basket with balls- BASKET-A and BASKET-B . Each basket contains 3 blue balls and 2 green balls . You select 1 ball from a Basket .What’s the probability of selecting a Blue ball ? (Conditional Probability Question)
Ans : Here, The Probability of picking Basket-A = 1/2 . Probability of picking Basket-B = 1/2 . Probability of selecting a Blue ball from Basket-A = 3/5 . Probability of selecting a Blue ball from Basket-B= 3/5 .
P( Selecting Blue Ball ) = P(blue Ball, Basket-A is selected first ) + P(blue Ball , Basket-B is selected first )
Final Ans = 3/5*1/2 + 3/5*1/2 (I hope you got this)
Converting the above conditional Probability Question into a Bayes !!
Q. There are 2 basket with balls- BASKET-A and BASKET-B . Each basket contains 3 blue balls and 2 green balls . You select 1 ball from a Basket and found that it’s a Blue Ball. What is the probability that its from Basket-A? (Bayes Question)
P(Basket-A | Blue Ball )= P(Blue Ball | Basket-A)* P(Basket-A)/P(Blue Ball)
P(Blue Ball ) = 3/5*1/2 + 3/5*1/2 (Calculated above in question)
P(Basket-A) = 1/2
P(Blue Ball | given Basket-A is selected ) = 1/2*3/5
Final Answer ( Simply put values in formula )= (3/10 * 1/2 )/(6/10)
You can also visualise the entire scenario by making a probability tree. (The image at the top) and then calculate evertyhing .
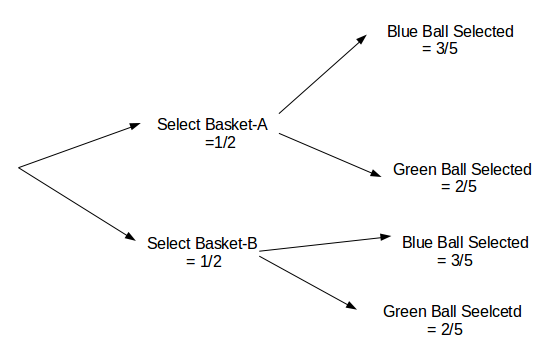 Visualisation Tree for Bayes Theorem
Visualisation Tree for Bayes Theorem
I hope you liked my post . Please give it a clap. It would encourage me to write more . If you are new to ml or Data Science, feel free to read my other post on machine learning by clicking on the link below .
Once Again, thank you for reading my post and don’t forget to Clap Share and Follow ..
Probability for Machine Learning was originally published in HackerNoon.com on Medium, where people are continuing the conversation by highlighting and responding to this story.
Disclaimer
The views and opinions expressed in this article are solely those of the authors and do not reflect the views of Bitcoin Insider. Every investment and trading move involves risk - this is especially true for cryptocurrencies given their volatility. We strongly advise our readers to conduct their own research when making a decision.