Transfer Learning : Approaches and Empirical Observations

Transfer Learning : Approaches and Empirical Insights

If data is currency, then transfer learning is a messiah for the poors

While there is no dearth of learning resources on this topic, only a few of them could couple the theoretical and empirical parts together and be intuitive enough. The reason ?? I guess we don’t transfer the knowledge in the exact way we store it in our minds. I believe that presenting complex topics in simple ways is an art, so lets master it.

Lets begin a series of blogs where we will try to discuss why the things are the way they are and the intuitions behind them in the domain of machine learning. The first in the line is Transfer Learning (TL). We will begin with a crisp intro about TL followed by problem statement which I solved. We will see how TL can be implemented through various ways in Tensorflow and study how each of the tuning parameters in the context of TL affect the model statistics (the most interesting part !!). Finally we will see the conclusions, tips and tricks followed by some of the best references I could find.

Introduction

A good naive definition looks like : “It is the ability to transfer knowledge from one domain to another” . Technically, it is: “ using weights trained on one setting (Task 1) to fit a model on another setting (Task 2)”. We generally use transfer learning when:

1. Dataset for Task 2 is small but we still want to train a model. (Presence of small data is not the only case when we would want to use TL, as we shall see later)
2. Both Task 1 and Task 2 are similar ie they have similar low-level features. More similar the tasks are, more applicable this concept is.

Transfer learning can be applied across various domains but we will restrict our discussion in the context of images.

Based on Similarity and Amount of data available , below are the approaches for different scenarios.

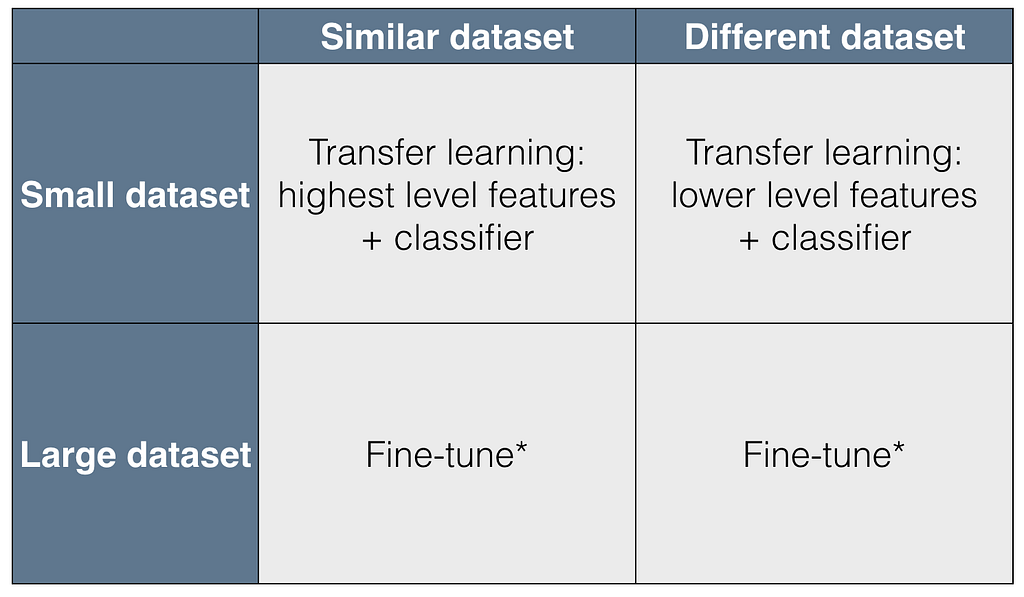Figure 1 : Different approaches in Transfer Learning based on type of datasets (Source : cs231n.github.io)

But before going deeper into these approaches, lets study the two major ways in which we can use Transfer Learning :

1. Use the original model architecture as a feature extractor and build upon them. This is similar to what we generally do in case of a typical machine learning problem. We manually engineer features and feed them to our model. But in this case, the heavy lifting of feature engineering is done by the pretrained model based on what it has learned (by learning , we always refer to the weights). Once you get the extracted features , you can feed them to your own new model. So the last point of previous model becomes the input for your next one. You can call this “plug and play model”. Just remove the top layer, add a new one in place of it. And voila !!! , you have got a new model ready.
2. Finetune the pretrained weights . In the above case, we didn’t attempt to modify the weights, rather they were used as it is for feature extraction. But this is not what we want in case the images are bit different. We would like the model to relearn some or all of the features it has learned. But isn’t it similar to training from scratch ?? No it is not. An example would make it clear. Lets say I have learned how to write “E”. Now I want to learn to write “F”. Should I relearn everything from scratch ie what is a straight line etc?? No. I just have to erase pixels of the lower edge and I have learnt a new letter.

So intuitively, the first case should be used if you are confident that the low level features for both tasks are same. If you are not, you might want to fine tune the model.

In some cases, even both of these are used together. Some part of the model is kept as it is whereas some of it is fine tuned. Just hold on, you will find detailed visual examples later.

Coming back to the four different scenarios, here is how we tackle them :

1. Task 2 has smaller dataset and similar to Task 1:

Fine tuning here is not a good idea because the model will overfit since the new gradients are calculated based on a much less (diverse) data. Doubts ?? . Just imagine that the pretrained weights are some random weights. Then it boils down to usual deep learning scenario. If you feed less data, it will overfit. More similar the images, more the pretrained weights will help you in avoiding overfitting , and hence lesser the sample you can do away with.

So it is preferred to use the weights for extracting feature and then training a classifier on top of it.

2. Task 2 has smaller dataset but different to Task 1:

Okay lets see. You can’t use fine tuning because data is small. And you can’t use features from top layer because the images are different (features from top layers are specific) . Now what ?? You can follow the same intuition above and extract features from not the penultimate layer but the pre-penultimate one (not sure if this is even a word :P). This is because the features from this layer will be more generic as compared to the ones from output layer.

3. Task 2 has larger dataset and similar to Task 1: Feel free to fine tune.

4. Task 2 has larger dataset and different to Task 1: Again, fine tuning is the way to go. But guess what, you can train a new model from scratch with that amount of data. :P

Now, lets begin with our problem statement.

Problem Statement

To perform OCR using Transfer Learning .

Task A: An image containing string of 5 characters. The original model could perform OCR with 99% accuracy. The weights were stored and later used for Task B. This dataset had 100,000 samples, sufficient to train a model from scratch.

Figure 2: Sample Images for Task A

Task B: An image containing string of 6 characters. Apart from length, one big difference is the type of noise present in both the images. Training data for this one, as a contrast had only 200 samples !!!

Figure 3: Sample Images for Task B

Impressed ? If you are thinking that we can perform any OCR using the training done on any other OCR samples, then there are some nice pointers for you.

There are some important behind-the-scenes steps/facts that make this work.

1. Noise removal : The first one is to bring the Task 2 image to the same standards as the Task 1. By standards I mean noise removal. Just like you can’t excel in Maths Exam by reading Sanskrit, in the same way you can’t expect the model to predict on the basis of features it has never seen (or seen very less). For eg: the different thickness of characters in the second image is new to the model as a feature. Remember : More such differences, more it is difficult for the model to adapt to the new case.

2. Input size : This is where we don’t have much control. First things first :

Number of parameters learned ∝ Size of input image

So the pretrained weight matrix we want to use has dimensions according to the first image. But guess what … both the images are of different sizes. To state it more intuitively: We are asking the model to give values of the parameters it has never seen and therefore never calculated. And hence the second image was resized and modified (added extra rows of white pixels) to match the original one.

3. Classes : This is similar to maths-sanskrit example. You can’t expect the model to predict “A” if the only thing it has learned is “a”. And this is true for any two cases where you want to apply transfer learning. Since the possible characters are same for both the images ie [a-z] we could use it without any second thought.

Implementation

Finally its time. The architecture for the model A is shown below. It has 3 Convolution layers followed by 3 fully connected layers.

Figure 4: Network Architecture for Task A

We will go through two approaches by which we can implement this concept.

Approach 1

Restoring the weights:

If you want to know the basics of storing and restoring tensorflow weight files, this is a very good article.

Next, we extract the value (weights) of all those variables / parameters that we are going to use in the Model B. Remember, the model architecture for Task B is same as that of Task A upto the Bottleneck Layer. Bottleneck layer is the one beyond which the architecture of model B differs from model A. So the weights for layers after bottleneck layer are not useful(atleast in our case, otherwise it depends on the tasks. A comparision is shown towards the end of this blog).

Lets get the values of pretrained variables.

tf.trainable_variables() gives all those variables which were trained in the model A. This includes all the Weight matrices as well as the Biases. So tf.trainable_variables() in our case gives the following output:

conv2d/kernel:0conv2d/bias:0conv2d_1/kernel:0conv2d_1/bias:0conv2d_2/kernel:0conv2d_2/bias:0dense/kernel:0dense/bias:0dense_1/kernel:0dense_1/bias:0dense_2/kernel:0dense_2/bias:0

As you can see, there are two parts to each variable name. First part is the name of the layer where that variable is defined followed by the type of the variable ie Kernel (usual weight matrix) or Bias.

Coming back to the bottleneck layer, it is the penultimate layer , the one just before the output layer in our case. The variables restored in previous step are the ones corresponding to the red portion (shown below). This portion is what we call feature extractor part of the model. The Green portion is the actual classifier which does the final job of classification.

Figure 5: Red portion is responsible for feature extraction and the Green portion does the classification.

The feature extractor has more to it. It can further be divided into two sets of layers. One set is frozen (R for Red), that is it’s weights don’t change . Second one (B for Blue) is where we do the fine tuning.

Figure 6: Red Portion refers to the frozen layers. Blue portion refers to the layers which are fine tuned.

Number of layers we want to fine tune (B) vs the ones we want to remain same (R) will depend on the similarity. Below figures represent different scenarios in the decreasing order of similarity. Top most refers to the case where images are almost same.

Figure 7: Both tasks are similar. No need to change the pretrained weights (Hence no B and only R)Figure 8: The Tasks are a bit different but not completely. So we can use low level features as they are (R) and fine tune the upper ones (B)Figure 9: Variation of the above caseFigure 10: Tasks are very different. So we don’t want to use any of the pretrained weights as such. So we fine tune them and hence only B.

So which one we are going to use for our case ?? The last one.

Modification of green portion is quite intuitive. Since word lengths of both tasks are different along with other dissimilarities, the original classifier needs to re-learn to output 6 letters instead of 5. The input to this classifier is the features extracted till bottleneck layer (ie through R and B)

The architecture (ie number of layers and their neurons) should remain same for the R and B portion because the dimensions of weight matrix restored should be compatible with it. The Green portion, however , can differ from the original model. For us, we don’t need extra layers. Only the output layers neurons need to be modified.

This is how model of Task B looks like (Figure 11). Each layer remains same (the architecture , not the weights) except the output layer.

Figure 11: Model architecure for Task B

So we fine tune the weights of all the layers for our case. But what about the weights of Green portion ? Do we fine tune pretrained weights for this portion also or we just initialize them randomly? More on this later.

Lets continue with the code.

Defining the layers

The 1st Convolution Layer in the original model which was used to train Task 1 is as follows:

The same layer , when being used for Task 2 looks like:

The added parameters are: kernel_initializer , bias_initializer, and trainable . The first two are used to initialize the kernel and bias weights with the pretrained ones. Whereas the third one is to state whether we want to modify weights of this layer.

If we want to do Fine tuning ie the B portion, trainable = True, otherwise it is False if want to freeze the weights and use this layer as it is, the R portion.

Approach 2

The steps for importing the graph and initializing the weights with the pretrained ones remains same as above except trainable parameter , the alternative of which is given below. The second approach to selectively train and freeze the layers is below:

train_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,scope="dense[12]")

training_op = optimizer.minimize(loss, var_list=train_vars)

Lets assume that we want to train only the output and penultimate layer while freezing the lower ones. The first line gets the list of all variables in dense layers 1 and 2 (penultimate and output layer) which are the ones to be trained. This leaves out the variables in rest of the layers. Next we pro‐vide this restricted list of trainable variables to the optimizer’s minimize(). Rest of the layers are are now frozen: they will not budge during training (these are the the frozen layers).

Observations

Enough of theory . Its time for some exciting stuff. Lets tweak some common parameters, compare and study their effects by plotting graphs.

Let me first describe the legends; Accuracy is being calculated over two levels :Character level (Orange line)= Number of characters correctly predicted / Total number of characters in samples Word level (Green line)= Number of entire words correctly predicted / Total number of samples

Eg: if actual word is “xmladj” and the predicted one is “xmladt”, then the word level accuracy = 0 and character accuracy is 5/6. The Blue line represents character level training accuracy. So, in short you would like to observe the mainly Green line. Lets begin !!

1. Effect of number of trainable layers

Left : Only the last layer is trained. Rest all are frozen.Right : All the layers are made trainable and are fine tuned.

Intuition:Since the images are quite different, retraining only the output layer is not sufficient (Left). A slight change in the low-level features is also required , hence fine tuning all the layers did the job (Right).

2. Effect of Learning rate

Left : Learning rate = 0.001.Right : Learning rate = 0.0001.

Intuition:Learning rate guides how big steps we are taking towards the optimum point. A lower learning rate (R) took more number of epochs but converged as good as the one with larger rate. But generally its preferred to keep learning rate for Task 2 smaller than what was used for Task 1. This is to ensure that the large gradient updates don’t distort the pretrained weight values. So we first allow the weights to stabilize and then let it propagate towards the inner layers.

3. Last layer initialised vs not initialised

For both the cases, all layers but the output layer are frozen.Left : Even the output layer is initialized with the pretrained weights and fine tuned.Right : The output layer is trained from scratch ie with random initial weights.

Intuition:Wait. What ?? The graphs are exactly the same !!. So interestingly, this means that pretrained weights (L) did no better than the random weights (R) for the output layer. And this is because the images were different enough so as to render the pretrained weights useless.

4. Effect of number of samples

Left : Number of samples 50Right : Number of samples 200

Intuition:It seems that number of samples didn’t make any difference in overall accuracy since the difference between the numbers is not huge. But the thing worth noting is the huge amount of fluctuations in test accuracy for the case of 50 samples in comparison to the one with 200 samples. This is because the batch size was the same as the number of samples. And since the smaller batch size leads to more frequent weight updates without observing reasonably good amount of data, the model could not be certain about it’s predictions, hence this observation.

Summary

1. Usually, the output layer of the original model should be replaced since it is most likely not useful at all for the new task, and it may not even have the right number of outputs for the new task.
2. Similarly, the upper hidden layers of the original model are less likely to be as useful as the lower layers, since the high-level features that are most useful for the new task may differ significantly from the ones that were most useful for the original task. You want to find the right number of layers to reuse.
3. Try freezing all the copied layers first, then train your model and see how it performs. Then try unfreezing one or two of the top hidden layers to let backpropagation tweak them and see if performance improves. The more training data you have, the more layers you can unfreeze.
4. If you still cannot get good performance, and you have little training data, try dropping the top hidden layer(s) and freeze all remaining hidden layers again. You can iterate until you find the right number of layers to reuse. If you have plenty of training data, you may try replacing the top hidden layers instead of dropping them, and even add more hidden layers.

References

Some of the best resources I could find:

Blogs:

1. Stanford’s CS231n : http://cs231n.github.io/transfer-learning/
2. Sebastian Ruder : http://ruder.io/transfer-learning/. A good starting point for Transfer Learning.
3. http://cv-tricks.com/tensorflow-tutorial/save-restore-tensorflow-models-quick-complete-tutorial/ . Good tutorial on saving and restoring tensorflow models.

Papers:

1. How transferable are features in deep neural networks
2. A survey on transfer learning

Books:

1. Hands-On Machine Learning with Scikit-Learn and Tensor Flow by AurElien Geron. This book has a good intro about Transfer Learning.

That’s not all. But enough to get you started . If you feel I have missed something or you have any clarifications, please drop in your comments.

And yes, don’t forget to Transfer your Learning of Transfer Learning.

Transfer Learning : Approaches and Empirical Observations was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.