Monkey Thinking

Without a doubt this is my favourite song and since hearing it first in late 2013, I’ve probably listened to it a few times each week since. It was during one of those weeks that I started working on a feature for a programming-project that heavily uses natural-language processing/understanding and it was during this song, that I asked myself:

What’s the difference with how I hear this song and how the computer hears it?

The key in answering this is to first consider how computers attempt to emulate our own physiological processes when we hear the opening line, “Have you got colour in your cheeks’…”. So, how do we hear that?

When Matt Helders (the drummer in the Arctic Monkeys) starts with the following…

BD = Bass Drum, FT = Floor Tom, HC = Hand Clap

…we can visualise the sticks hitting the bass drum on every beat. Imagine if that bass drum was a bucket of water and with each beat you hit its surface. You can already see the splash launching up at you. Sound waves exist in a similar way because they’re caused by collisions (loosely). Specifically, it’s the vibrations from a source that traverses across a medium and consequently prompts every particle within that medium to undergo the same motion.

As waves change the position of particles, they’re effectively changing the pressure within this medium or in other words, they’re creating pressure fluctuations.

To visualise this, consider a piston in an internal-combustion engine. As the piston rises into the cylinder, you have to be able to see that the amount of free space in the cylinder decreases as the piston rises further into the cylinder. Alternatively, if you drop an apple into a full glass of water then there’s going to be an overflow of water because clearly multiple particles can’t exist in the same position at the same time.

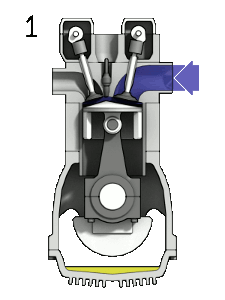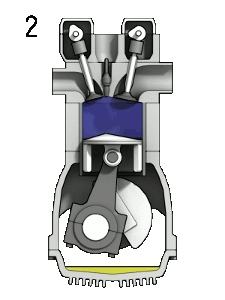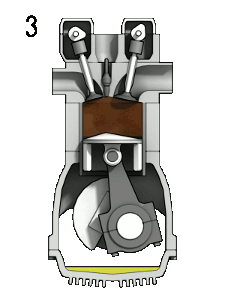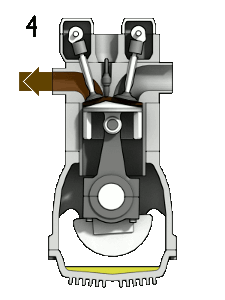A four-stroke internal-combustion engine. (1) Fuel in as the piston moves down and creates a partial vacuum in the cylinder, (2) piston compresses the fuel, (3) spark-plugs ignite the fuel and the resulting combustion pushes the piston back down called the “power-stroke” that in effect turns the crankshaft that’s connected to the base of the piston, (4) exhaust is expelled and new fuel enters the cylinder.

We now know that as the wave propagates across the medium, the particles are going to move and hence change the pressure with respect to that region. It’s these pressure fluctuations that allows us to hear.

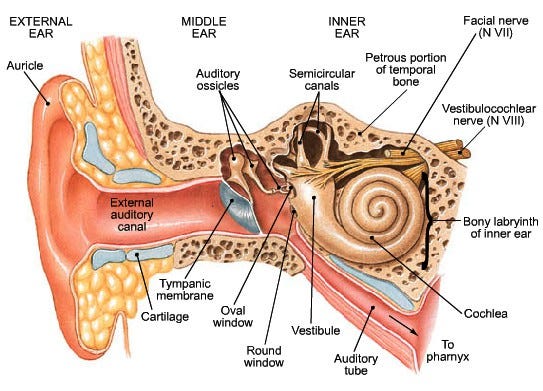Imagine the process of “hearing” begins at the far-left of the image, with the sound-waves hitting the auricle and echoing into the external auditory canal and so on. By following this linear direction, you’ll see how the sound wave eventually reaches the Vestibulocochlear nerve.

Sound-waves cause your eardrum to vibrate and because objects that vibrate are the source of waves, vibrations are felt elsewhere in your body. As the wave hits your tympanic membrane, the eardrum, these vibrations are subsequently felt by the three smallest bones in your body that are collectively called the Ossicles.These bones amplify the sound vibrations and send them to the cochlea in the inner ear.

The cochlea is a snail-shell-shaped organ that’s responsible for converting sound into electrical signals that can be processed by the brain. Sound travels through the cochlea due to the fluid, endolymph and it’s the electric potential (how much energy a charge will gain/lose based on its position with respect to this source) of endolymph that makes it so important for the neuronal encoding of sound.

The body, and so the brain, rely on electric currents for functionality. Currents describe the flow of electrons between opposing charges. Whenever positive and negative charges are separated, energy is expended. Voltage is a measure of this separation. The resulting charges are brought into motion because positive and negative forces attract one another. You can see the idea of this attraction in action with magnets.

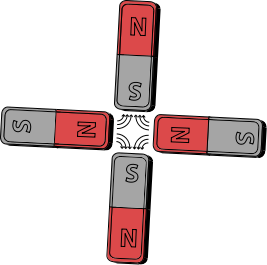This is a pretty ballsy image to describe electromagnetic forces if you’re unfamiliar with them but if you can convince yourself that magnets with the same polarity (N or S) repel and then that the inverse polarity attracts that magnet, then you’re doing well.

Electric charges exist in discrete quantities that are all integral (whole, positive numbers eg. 1, 2, 3,….to positive-infinite) multiples of 1.6022 X 10-¹⁹ Coloumb. To avoid recursively providing definitions, let’s just keep our Coulomb definition as being 6.24 x 10¹⁸ electrons.

So we now know that when charges are separated, energy is expended. When these charges move, they create a current. With a current, we can move energy.

With this in mind, let’s return to our endolymph that fills our cochlea. Lining the walls of the cochlea are mechanosensory cells. Projecting from mechanosensory cells body are slender “arms” that are called stereocilia. These are organised with the shortest stereocilia on the outer edge of the mechanosensory cells and the longest toward the centre. As a cross-section, these would look like a triangle. As a side note, because of this evolutionary design, these sensory cells can “tune” to different sound waves.

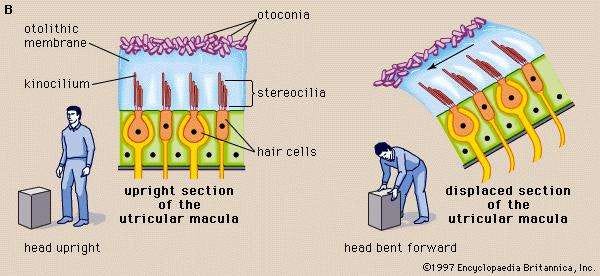On a further side-note, it’s because the stereocilia move when your body moves that we can understand our position in 3d-space. This is why people with ear infections might have trouble balancing!

Now, because of the high concentration of positive potassium ions in endolymph, its electric potential of 80–120 mV makes it uniquely higher than anywhere else in the body. That’s to say, the largest electric potential difference can be found in the cochlea. This property is important so keep it in mind.

As sound-waves cause vibrations, this can cause ripples in a liquid. So when sound moves past your ear drum and hits the basilar membrane in the Organ of Corti within your cochlea, the resulting vibrations move the endolymph. These movements are felt by the 32,000 mechanosensory cells that line the cochlea and the consequence is analogous to flicking on a switch in a room — when mechanosensory cells are excited, they send strong (high electrical potential thanks to the potassium-rich endolymph in the cochlea) and sensitive (the ordered stereocilia that protrude from the mechanosensory cells can be attuned to different frequencies) signals to the cochlear nerve that connects to the brain.

Remember that so far we’ve only discussed the mechanical translation of a sound-wave to an electrical signal. That signal now needs to be processed by the brain.

To really hone in on the marvel of biological engineering, here’s a video that shows the brain from an autopsy of a recently deceased patient. It’s one of the few videos/images online that you can find of what the brain really looks like.

To give some context about human-brains, they’re approximately 1200cm³ in volume (a professional soccer-ball is about 5575 cm³), contain about 90 billion neurons (a fruit-fly has about 250,000 and an African Elephant has 250 billion), and approximately makes ~10¹⁴ operations per second (that is, our brains makes ~10¹⁴ decisions per second).

With respect to how the brain works there’s a lot of ambiguity. I’ve found it quite surprising how little we really know how the brain works because there’s a lot of “black-box” descriptions. So without going into too much technical detail I’m going to provide a few interesting notes that highlight neurological functionality without requiring too much neuroscientific understanding.

ModularityA symptom of severe herpes is an inability to identify animals. This relates to how the brain has a somewhat modular design, with different regions of the brain relating to different functions. For a high-level description of the brain, we consider four-different lobes; the occipital (generally related to vision), temporal (emotions, memories), parietal (coordination, movement) and the frontal (planning, evaluating). Herpes can attack the olfactory nerve that’s connected to our nose. Near the olfactory nerve is a region of the temporal lobe that’s theorised to store memories of animals. There’s varying arguments for why this is, with one (but now largely dismissed) idea suggesting that because the brain evolved across evolution, the regions closer to the brain-stem are perhaps the more primitive versions of our brains and hence contain the neurological behaviour of our primitive ancestors such as the Neanderthals, Homohabilis and even Chimpanzees.

The way our brains encode behaviour and learn to process our surroundings is an incredible process to consider. For instance, if we look into the case of Genie, a young American child that was effectively tied to a bed in a pitch-black room for the first 13-years of her life, we see (1) how our childhood experiences create our adult brains and (2) the irreversible damage childhood experiences can have. Genie was never able to speak a first-language and is considered highly-socially impaired.

This idea of modularity also explains neurological conditions like Alexia Sine Aphasia — when a patient can write their name but be unable to read what they just wrote because they’re unable to understand writing. Reasons for this generally converge on the belief that because writing is relatively young — 5,000 years ago, our brains have yet to mature to this new behaviour and therefore have far limited access to neurological resources.

Biological + Physiological + PsychologicalDid you know there’s only been one disease that’s actually been entirely eradicated? That’s Kuru. During the 1950s, there were increasing reports coming from Papau New Guinea of a bizarre disease that seemed to be only affecting the 40,000-strong Fore tribe. Symptoms began with decreased muscle control (similar to Parkinsons) that would later develop into a complete inability to walk/control bowels and in the terminal stage, the victim would usually be unable to swallow or be responsive to their surroundings despite being able to maintain consciousness. There were initially a lot of different theories as to what could be causing Kuru but it took the genius, resilience and complex (we’ll later learn why) behaviour of an American doctor, Dr. Daniel Gajdusek to start piecing the story together. There were a few clues, firstly it was discovered that Kuru victims had tiny “scars” in their brains caused by dead astrocytes, a type of glial cells that protected the brain in forming the blood-brain-barrier, a protective coating around blood vessels that blocks foreign substances from entering the brain. Astrocytes exponentially multiply when neurons die, which eventually cause scars on the brain.

Those black dots…yeah they’re holes created by dead neurons.

But it wasn’t until researchers mixed part of a Kuru victim’s brain with water and injected the resulting mixture into a chimp that there was a real breakthrough. After performing autopsies, the researchers found that Kuru was not a genetic disease but instead contagious amongst primates. What was more startling was that it took 3 years from the injection till the chimp began showing severe symptoms of Kuru disease. This led to the discovery of “slow viruses”, a type of disease that after a period of latency, slowly evolves within the victim. What caused this slow-virus remained elusive to researchers for years. For example, neural tissue infected with Kuru could be roasted in ovens, soaked in caustic chemicals, fried with UV light, dehydrated like beef jerky and exposed to nuclear radiation — and still remain contagious. Because no living cell could survive such an onslaught, it led researchers to believe that proteins (respectively considered non-living compared to other types of cells), could be the source. Because proteins are simpler than other cells, it was thought that they could survive sterilisation, pass the blood-brain-barrier easier and avoid triggering inflammation because they don’t have the markers that immune cells use to identify threats. Specifically, these type of rogue proteins were called prions and it was later found that normal brains manufactured proteins and prions in the exact same way. So what distinguished prions from healthy proteins? It was their 3D-shape. Just how different objects can be created with the same LEGO bricks, proteins are defined by their 3D-shape. It was a crucial corkscrew-shaped stretch that were usually found in proteins, but instead was mangled and refolded in prions that caused their distinction. As for what prompted Kuru to spread, well unfortunately the Fore tribe had a thing for cannibalism in the early decades of the 1900s and as a slow-virus, it only came into effect long after the victim had basically eaten the contagious neural-tissue. There’s a lot of important ideas here: we’ve seen how devastating neurological conditions can be, the nuanced states of proteins and the type of defences the brain has in protecting us from alien materials. To me, this anecdote highlight perhaps the most important understanding about the brain: brain functionality is explained by a combination of biological, physiological and psychological operations. As for Dr. Gajdusek, he was charged with child molestation in 1996 and would later die in self-imposed exile in 2008.

Hyper-specific purposeNeurons have specific neurological purposes — and I mean really, really, really specific purposes. In a research-project that would lead them to Nobel Prizes, David Hubel and Torsten Wiesel strapped cats into a fixed-position and showed them different images to research how the primary visual cortex works by using electroencephalography (measuring electrical signals when neurons were triggered). The story goes that for literally months, these cats would be strapped into a fixed position and shown slide after slide with the researchers hoping to detect some sort of signal. It wasn’t until one of the researchers accidentally jammed a slide into the projector, causing the slide to be diagonally inserted, that a signal was detected. It was the angled-line that prompted the spike.

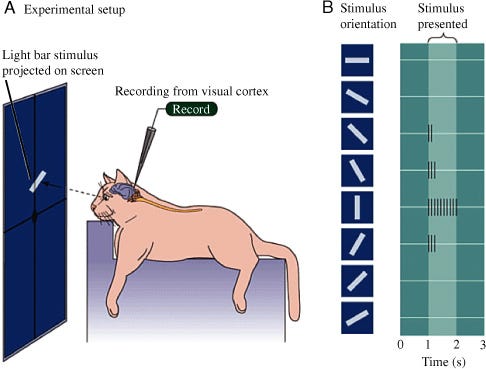In further research, it was discovered that the brain finds it easier to detect moving images as opposed to still images. Because of this it’s possible to stabilise an image causing your brain to think there’s nothing there!

What Hubel and Wiesel accidentally realised was that the brain breaks down images into arrangements of lines and that an individual neuron in the primary visual cortex is responsible for a single “line” in 2D-space. Neurons are stacked on one another, in an arrangement called “hypercolumns”. At the top of this hypercolumn is the neuron responsible for the line vertically orientated and as you descend through a hypercolumn, you rotate the line until you reach a complete revolution. The brain not only has logical categorisations within, but brain functionality can be a function of what has been experienced before.

There was a lot to take in just then but to say “hey let’s talk about the brain” without some firm preparation would’ve made the following redundant.

To recap, by a sound-wave coming into contact with the stereocilia, we’ve initiated a process called mechanotransduction where a mechanical stimulus is converted into electrochemical energy. Within the ear this is a highly sensitive process — small fluid fluctuations of 0.3 nanometres can be converted into a nerve impulse in about 10 microseconds.

Specifically, the stereocilia cells release a neurotransmitter at synapses with the fibres of the auditory nerve, which in effect produces action potentials (a voltage).

There’s been a lot of research into addiction that’s involved analysing the structures of neurons. For patients that suffer from addiction or are genetically inclined towards addictive behaviour, it’s been discovered that their axons/dendrites form stronger bonds with the axons/dendrites of other neurons. This is how neurons communicate — by sending electrochemical signals from one end of the neuron, to the other and the space between two neurons is called the synapse.

The auditory nerve transmits its signal to the auditory cortex which is found in the temporal lobe. Neurons within the auditory cortex are organised by the frequency of sound they respond to best with neurons at one end responsible for high frequencies and at the other, neurons for low frequencies. Just like the visual cortex, it’s possible to create a frequency map (tonotopic map) — that is, map neurons to the frequencies we hear.

What exactly happens within the auditory cortex isn’t entirely known — largely because how your brain works can be quite different to how mine works. There are however some high-level assertions we can make.

Language is processed in multiple regions and simultaneously within the auditory system that includes the auditory cortex. Signals from the auditory cortex are passed onto other regions, and these include the Wernicke’s area, and Broca’s area. Just to emphasise how different brains can be — the regions used to understand speech — are found in the right hemisphere of 97% of people. Not everyone has the same brain.

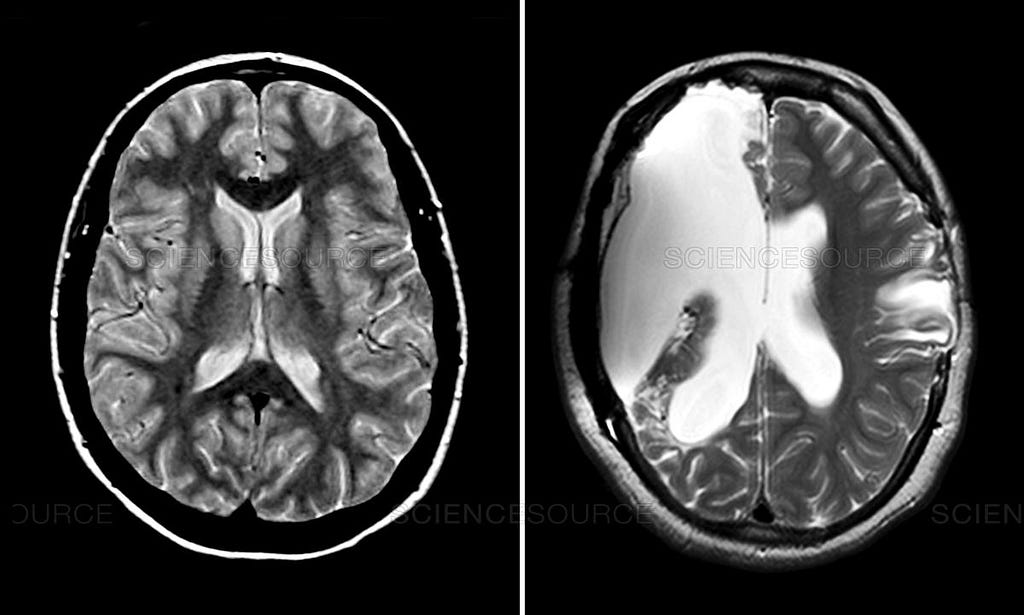In another example of how unique brains can be, the above shows a comparison between the cross-section of a normal brain (L) and the cross-section of a brain after a hemispherectomy operation (R). The white-space in the right-image is cerebrospinal fluid floating where the left-hemisphere used to be. That’s because a hemispherectomy is when one hemisphere of the brain is disconnected from the other and then sometimes, entirely removed. It’s a surgical procedure used for children under the age of 6 that suffer from intense magna-gal type seizures and thanks to neuroplasticity, a lot of the functionality that exists in the affected-hemisphere, can be rewired into the remaining hemisphere.

The Wernicke’s area is mostly responsible for processing speech and is involved in communicating with others while the Broca’s area is usually found to be responsible for speech production. In classic neuroscientific-ways, we generally only learn about the purpose of a region of the brain because of accidents/diseases affecting that region and hence correlating the subsequent behaviour to that region.

You might be thinking that the above was quite light in technical detail (at least I did) and there’s a reason for that — we don’t really know what goes on. There’s clearly an unbelievable amount of unknowns.

However — to say we don’t know how a computer hears “Have you got color in your cheeks…” is entirely false. Let’s now consider how a computer hears this song if we asked it to transcribe the sound to a text-based output.

Remember that electrical currents are electrons in motion. This proves to be critical in how computers work because at their most primitive state, it’s a series of existent/non-existent electrical currents that allow computers to operate the way they do.

We can see this idea in action with morse code.

We can expand this concept further, using patterns of signals to describe “ideas”. For instance, if I wanted to send “1” and my options for signals were either “0” or “1”, then “0” could simply be one signal and then “1” could be two-signals sent in succession.

We can string together more complex structures by taking advantage of binary and hexadecimal notation. There’s plenty of resources available online to describe how these work by comparison to the other topics we’ve discussed so far. With binary/hexadecimal representation, we can convert single characters into single binary/hexadecimal representations.

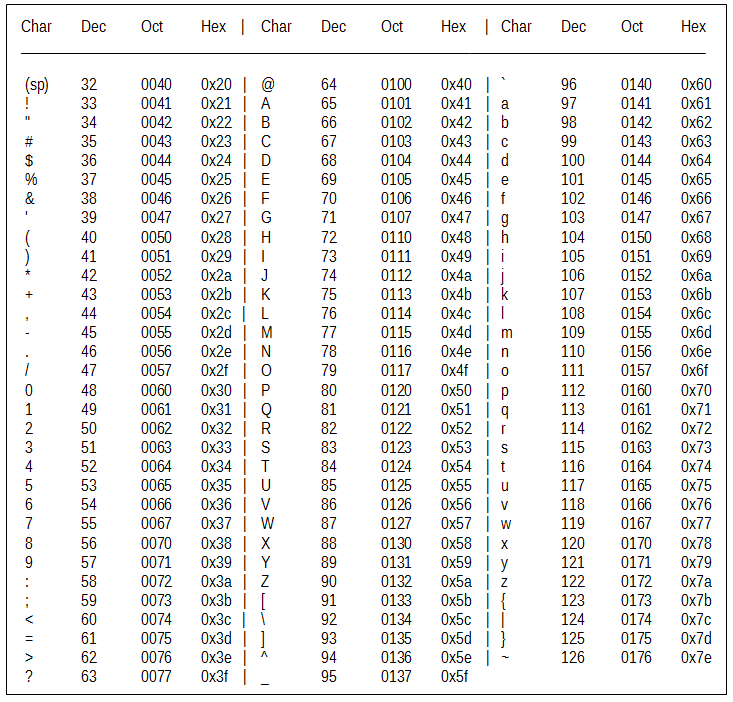ASCII is just one way to encode letters and digits into a decimal that can also be represented as hexadecimal number.

Let’s say we want to compare “15” with the number “10” — it would mean we need to compare the electrical signals that represent these digits. This leads us to combinational logic. Within computers, different bit values are represented as high (5V) or low (0V) voltages. This means that the number “15” in binary is “0000 1111” would be represented as a series of four low-voltages and then four high-voltages.

There’s a clear theme amongst classical computing and it’s the omnipotent binary status of information. It is, or it isn’t. This notion is the foundation of how we can check values against each other. Boolean algebra started with George Boole after he observed that by encoding True or False as 1 and 0 respectively, basic principles of logical reasoning could be shown.

For instance, if I ask to flip the value of “1” then I’ll have “0”. So if I ask if “1” equals “0” then the answer will be “0” because it’s false. We can extrapolate this thinking to reach the boolean logic operations, “AND, &”, “ OR, |”, “NOT, ~”, “EXCLUSIVE-OR, ^”. Take some time understanding the below table because it’s foundational for future operations.

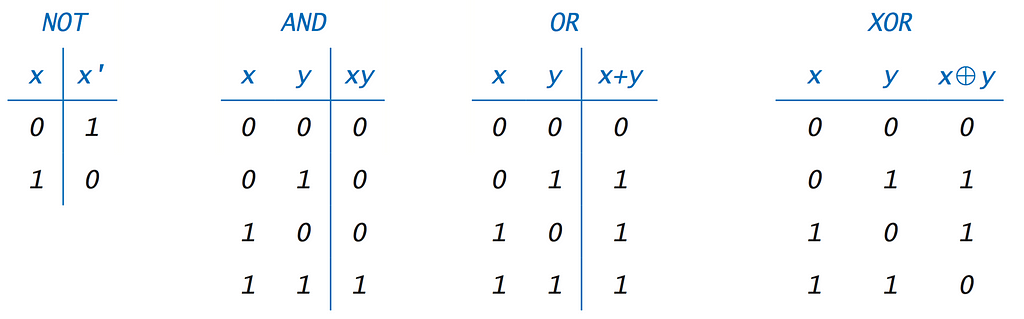For unary-operations, the first-column is the input and the second-column is the output. For binary operations, the left and centre columns are the input and the right column is the output.

To complete an AND operation in a computer we need to use the AND logic gate. These are found on the microprocessors that work in our laptops, phones, televisions and so on. For reference, a microprocessor looks like this:

Intel Xeon-E Processor: 6 cores, 6 threads, base-frequency of 3.4GHz, 19.25MB L3 cache with a maximum memory speed of 2666 MHz and capable of supporting a maximum RAM of 768GB. Ye, it’s a biggy.

Logic gates consist of transistors that receive an input-voltage that’s representative of either a high or low-voltage and then output a higher-voltage depending on the type of input-voltage. A typical type of transistor is the bipolar junction transistor and it operates like so:

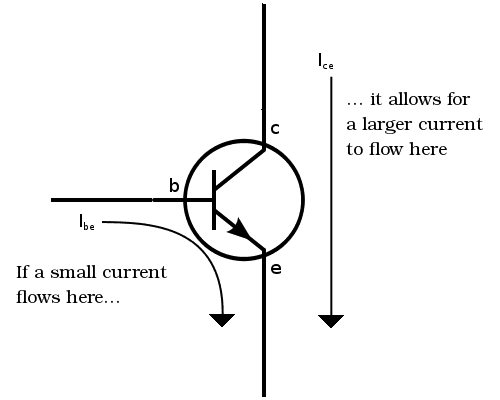An input current flows into the base (b) that opens the current from the collector (c) to the emitter (e). If we apply a high-voltage from the base, then we’ll get a much higher-voltage from the emitter.

So now we have a way to measure whether something is or isn’t there — the presence/absence of an electrical current. What we want to do now is combine these aforementioned rules and bring them together to form a system to compare values. This is called combinational circuits.

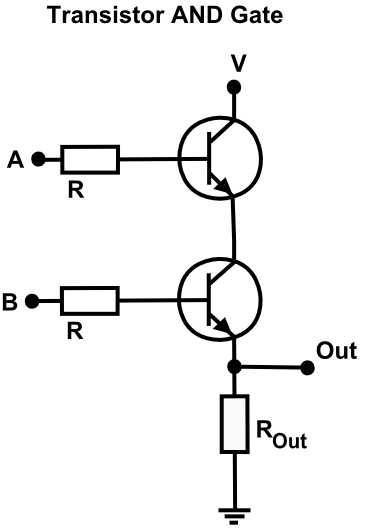Remember that an AND logic gate is comparing two values. We have input A and input B on the left, with their signals passing by two-resistors and then each entering a transistor that we described before. Because voltages are accumulative in series, we’ll be able to know whether both had the same value by noting the final voltage that’s outputted.

Now that we see how this AND gate works, we can consider it’s role in a combinational circuit involving two AND gates, an OR gate and two NOT gates.

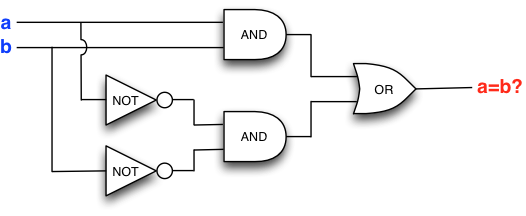This is the combinational circuit to test equality between two values. To convince yourself that this proves whether two values are equal, plug them through as simple “1” and “0” representations.

So now that we have a process to compare values and determine their relationships, we can execute operations. Think about how you could reduce any operation to a series of comparisons and if you think the computer doesn’t have enough time remember that the Intel Xeon -E can make 3.4 billion executions a second! In other words, it could send through 3.4 billion different combinations through the above equality combinational circuit every second!

In some instances we just need to simply execute this operation and move onto the next operation. But you can see that there’ll be times when we need to get the value from a previous result and use if for another. For instance, if we had the following series of operations:

1. Add 10 to 42,
2. Take the result of step1 and divide it by 4,
3. Take the result of step1 and multiply it by 10,
4. Take the results of step2 and step3 and subtract 99

Then it becomes clear that we need a way to store these values. Within computers there’s two different ways to store memory, through clocked-registers or Random Access Memory(RAM). Clocked-registers store individual bits (eg. for “15” that’s represented as “0000 1111”, the first-four registers would hold “0” and another-four would hold “1”), or words — the amount of bytes the microprocessor takes per operation. For a 64-bit system this is usually 8 bytes (8 x 8 = 64). As for why registers are called “clocked” — for each cycle of the processor, that is each time a new signal is sent through the processor (represented by the clock-speed, eg. for Intel Xeon-E this is 3.4 GHz), a new value enters each register. So for every second, each register in the Intel Xeon-E will receive 3.4 billion values.

Since we can represent values through electrical signals, it stands to reason that we can encode values and one of the ways we access the encoded values is through RAM. To understand the role of RAM we need to consider memory storage through hard drives. As most hard drives are following solid-state drives (SSD) architectures, we’ll focus on these. Say we way to encode “15” into our hard-drive and we know its binary representation, then all we need to do is assign a region of memory in this hard-drive to the bit-values. SSDs use transistors to store memory with the presence/absence of a current telling the system whether the contained value is a “1” or “0”.

A quick comparison between HDD and SSDs — typically the arm on a HDD rotates at 7500 RPM but because this is an inherently mechanical process there’s physical restrictions involved along with additional dangers, eg. you should never move a HDD while using it because it could damage the data stored on the disks.

So now that there’s an area on the computer that has permanently stored our value “15”, we can now retrieve it. However, to expect the computer to search through the entire memory of our hard-drive to find our value and operate at peak performance is a ludicrous expectation. Consider the data-servers at Facebook that contain the data of 2 billion monthly users. Every time you send a web-request (eg. login on Facebook, click the profile picture of someone you’re stalking, accidentally tap hello on that same person etc), Facebook will need to retrieve the relevant data to update your web-browser. Because we know memory is stored in cells, a fast way would be to have a map of all these addresses — and that’s exactly what RAM is. For websites such as Facebook, a rule of thumb is for the size of RAM to be at a minimum as large as the largest data-table so in that way it can instantly look up the address of where the relevant data is, as opposed to traversing through the entire contents.

Let’s now look at a high-level design for a classical computer:

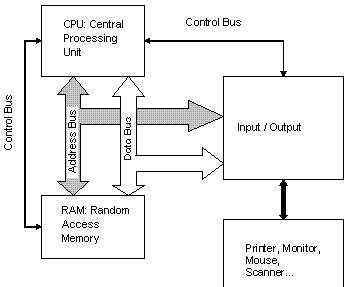This is a highly simplified illustration describing high-level computer architecture. The “Address Bus” relates to the addresses within our memory, and “Data Bus” relates to the data that’s held in the memory addresses.

We now have the hardware and the general system in place to begin executing our instructions. Hopefully it’s occurred to you by now that “instruction” is a pretty vague description for what’s really going on inside a computer.

Since computers operate on bits, we need a way to encode our instructions into a way that the computer can understand. That is, some instructions are going to have different purposes and involve different registers, memory cells, values and so on. How instructions are processed by computers are a highly-technical and designing these processes is quite a rare-opportunity comparatively speaking.

There’s a few underlining ideas here that we need to aggregate into one overarching architecture:

1. Computers operate on individual addresses,
2. Computers rely on instructions that contain a series of details that describe the operation to be executed,
3. Computers need to know their next instruction,

The answers to these ideas can be found in a computer’s Instruction Set Architecture (ISA). Within this, we have a number of different registers to be used for the instruction, a Program Counter (PC) to point the system to the next instruction and a Stack Pointer (SP) that points to the next available free-spot in a computer’s memory.

Within the ISA there’s a collection of primitive operations a computer can do, such as, stop execution (RET), move a value to another register (RRMOVQ), jump to another instruction (CALL), return the value at the most recent memory address (POP), add a value onto the next available memory address (PUSHQ) and so on.

Just as how we can encode words into binary representations through ASCII, we can encode the register details and instruction types as numbers too.

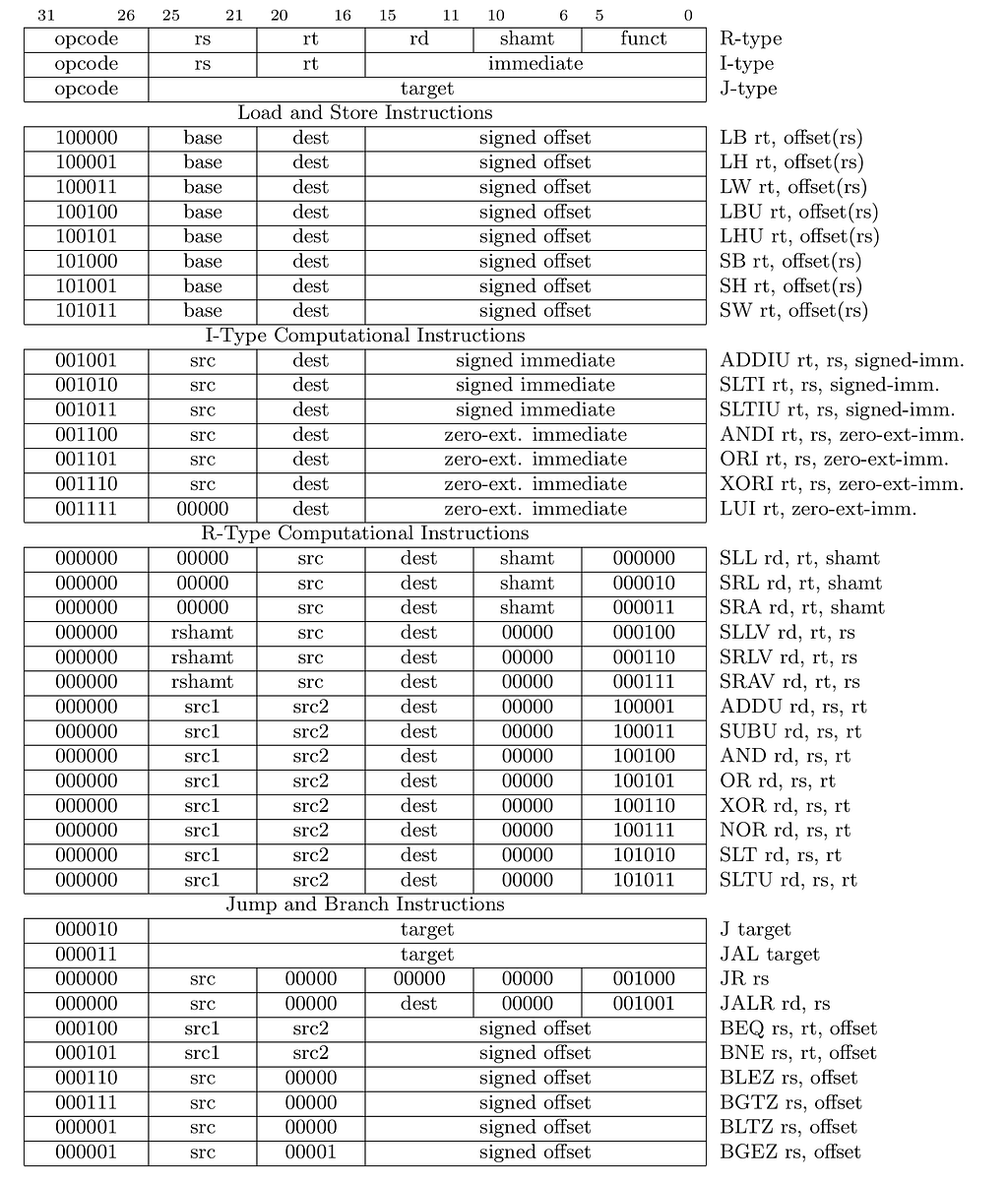You can see the OPCODE in the far-left column denoting the number for that instruction.

This means that our instruction has to go through some process that translates it into a form that the computer can understand.

Our instructions are typically inputted as a human-readable language. Some of these languages you may have heard of — Python, Java, C etc. For instance, the command to print “Have you got colour in your cheeks” in each language is as follows:

Python(3):

print(“Have you got colour in your cheeks”)

Java:

System.out.println(“Have you got colour in your cheeks”);

C:

printf(“Have you got colour in your cheeks”);

When we run the instructions, the system takes this readable command and translates it into assembly-code which we can see in the below image. From this assembly-code, it’s further translated into machine-code — a series of hexadecimal representations of each part of the assembly-code. The result is a stream of hexadecimals that is fed into our processor and by using the ISA, the instructions can be executed.

While you may not necessarily understand what’s going on above, it’s important to see how the assembly-language statements are translated into a hexadecimal representation.

We’re now at the stage where we can begin investigating how our computer will process “Do I Wanna Know” in a natural language processing/understanding context. For simplicity we won’t be analysing the semantics involved as we didn’t do so with the physiological-approach at the beginning.

Say we’ve written a series of instructions (a program) that takes in an audio file (“do_i_wanna_know.wav”) — the next step is for the program to determine the sounds in the file.

We’re starting to venture into machine-learning territory which deserves an entire article to itself so we won’t get too bogged down with details. In summary, we’ve taken inspiration as to how the auditory cortex responds to sound with neurons arranged by how they respond to different frequencies. In a similar way, programs can be designed to assign a value to different sounds within audio files. By decomposing words into a unit that’s similar to syllables we can create a series of patterns that describe how words are composed with respect to these base units.

For example, if we wanted to tell a computer how “five” sounded, we could describe it like so: “fy” + “ve”. Or for “ten” it could be “t” +“n”.

What we’re doing is designing a supervised machine learning solution that with the aid of a large dataset that has a large number (generally speaking in a professional context, for each unique classification you’d want a few thousand different examples), the system can overtime find a pattern amongst all these different combinations and create a process that identifies the words. We find these patterns by considering how far off the output is agains the true-classification for that word. So by running this system repeatedly, the system can overtime correct its mistakes and look into different patterns that might indicate a way to understand these values.

This is the process for Automatic Speech Recognition and it requires a lot of training data to generate decent results. Imagine having thousands of different examples for every possible word and then running all that data through the computer to find patterns.

Thankfully other people have done this for us — namely Google, Amazon and Microsoft, and provided APIs (keys for any programmer to interact with this software) that allow us to input our audio file and then run it through this ASR to receive a text-translation!

In this example I used Google’s Speech API and fed it a WAV, mono-channel file that was taken from the YouTube video at the beginning of this article. You can see the first minute or so of transcriptions a long with Google’s confidence rating:

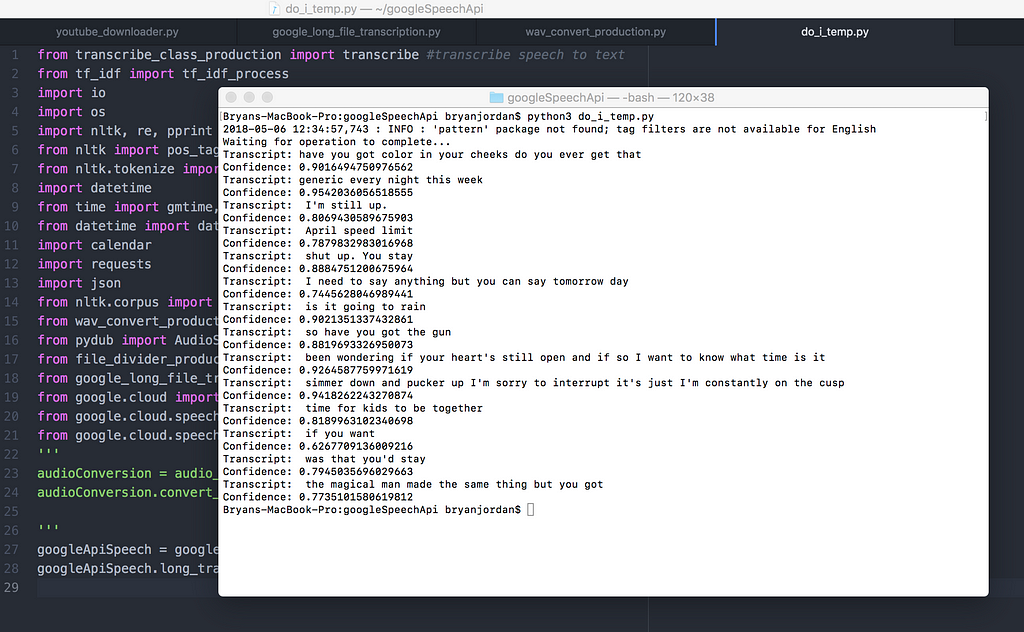I realised as this started transcribing that there was going to be A LOT of noise in the audio file. I mean quite literally. We weren’t inputting an audio file of just they lyrics but the entire song with the bass, lead guitars and percussion all included.

To wrap things up, take the opportunity to re-listen to the song while going through the lyrics and consider the differences between how you hear them verse how the computer does.

Everytime I do I can’t help but think computers could work a bit differently…

Monkey Thinking was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.