Consistent hashing with bounded loads, using a Red-Black Tree

In these series of articles, I would be implementing a few famous papers related to distributed systems, primarily in Golang.

This article deals with an approach to use a Red-Black tree (instead of a hash table) for building a consistent hashing library.

What is Consistent Hashing?

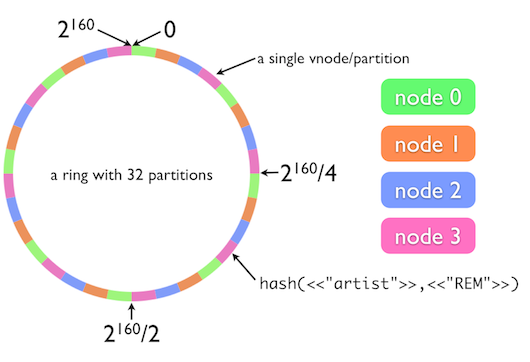
Consistent hashing is a special kind of hashing such that when a hash table is resized and consistent hashing is used, only K/n keys need to be remapped on average, where K is the number of keys, and n is the number of slots. I wouldn’t like to go into too much detail of how exactly consistent hashing helps, but here are few articles if you would like to know a bit more about it.

In most libraries, the implementation is done by using a list, to store all the keys in a sorted form, and a hash table to figure out which node the key belongs to. So a key which mapped on a circle could be easily mapped to the node by writing a simple search function, since the list is already sorted.

Here’s a simple implementation taken from groupcache (slightly modified for clarity):

Insertion:

To add the list of nodes to the ring hash, each one is hashed m.replicas times with slightly different names ( 0 node1, 1 node1, 2 node1, …). The hash values are added to the m.nodes slice and the mapping from hash value back to node is stored in m.hashMap. Finally the m.nodes slice is sorted so we can use a binary search during lookup.

func (m *Map) Add(nodes ...string) {    for _, n := range nodes {        for i := 0; i < m.replicas; i++ {            hash := int(m.hash([]byte(strconv.Itoa(i) + " " + n)))            m.nodes = append(m.nodes, hash)            m.hashMap[hash] = n        }    }    sort.Ints(m.nodes)}

Search:

To see which node a given key is stored on, it’s hashed into an integer. The sorted nodes slice is searched to see find the smallest node hash value larger than the key hash (with a special case if we need to wrap around to the start of the circle). That node hash is then looked up in the map to determine the node it came from.

func (m *Map) Get(key string) string {    hash := int(m.hash([]byte(key)))    idx := sort.Search(len(m.keys),        func(i int) bool { return m.keys[i] >= hash }    )    if idx == len(m.keys) {        idx = 0    }    return m.hashMap[m.keys[idx]]}

Why a Red-Black Tree?

Hash tables can look up any element in O(1) time, but self balancing trees have their own advantages over a hash table(depending on the use case) for the following reasons:

1. Self balancing trees are memory-efficient. They do not reserve more memory than they need to. For instance, if a hash function has a range R(h) = 0...100, then you need to allocate an array of 100 (pointers-to) elements, even if you are just hashing 20 elements. If you were to use a binary search tree to store the same information, you would only allocate as much space as you needed, as well as some metadata about links.
2. There is huge probability of collision as data grows. One of the ways to handle collision is Linear probing. It is a form of open addressing techniques. In these schemes, each cell of a hash table stores a single key–value pair. When the hash function causes a collision by mapping a new key to a cell of the hash table that is already occupied by another key, linear probing searches the table for the closest following free location and inserts the new key there. Lookups are performed in the same way, by searching the table sequentially starting at the position given by the hash function, until finding a cell with a matching key or an empty cell. In this case, worst time for insertion, search, or deletion is O(n).
3. Also a hash table needs to be assigned allocated space initially, more than the size of input data. Else the hash table bucket would need to be resized, which is an expensive operation if say there are millions of items being inserted into the hash table.
4. The elements stored in hash table are unsorted.

Though Hash Tables have their own advantages, I found a self balancing tree to suit well to the requirements of building a consistent hashing library. Most self balancing trees provide a lookup of O(log n) for insertion, search and deletion in worst case. And the elements are sorted whilst insertion, hence there is no need to re-sort an array every time an insertion happens.

Implementation

In this blogpost, folks from google have explained a slight variant to the original paper from akamai, for better uniformity and consistency in distribution of keys in the consistent hashing circle. Because of the advantages of a self balancing tree over a hash table, I thought of implementing this in Go.

Using a Red-Black tree, an insertion/search into the consistent hash circle ring would look like below:

Insertion:

func (r *Ring) Add(node string) {

for i := 0; i < r.virtualNodes; i++ {  vNodeKey := fmt.Sprintf("%s-%d", node, i)  r.nodeMap[vNodeKey] = newNode(vNodeKey)  hashKey := r.hash(vNodeKey)  r.store.Insert(hashKey, node) }}

Search:

And searching a key would be little complicated, but it is just as simple as traversing down the tree to find the element(node) greater than the key. Going around the consistent hash circle would be as simple as finding the successor of the nearest key in the Red-Black tree, and checking if the load is okay at the particular node for insertion, else we need to wrap around (reach the root), and try searching again till we find a node that is free to accept the request.

func (r *Ring) Get(key string) (string, error) {

var count intvar q *rbt.NodehashKey := r.hash(key)q = r.store.Nearest(hashKey)

for {

/* Avoid infinite recursion if all the servers are under heavy load  and if user forgot to call the Done() method*/  if count >= r.store.Size() {   return "", ERR_HEAVY_LOAD  }

if hashKey > q.GetKey() {   g := rbt.FindSuccessor(q)   if g != nil {    q = g   } else {    // If no successor found, return root(wrap around)    q = r.store.Root()   }  }

if r.loadOK(q.GetValue()) {   break  }  count++

h := rbt.FindSuccessor(q)  if h == nil {   //rewind to start of tree   q = r.store.Root()  } else {   q = h  } } return q.GetValue(), nil}

The complete code is available here.

arriqaaq/xring

Feel free to point out any errors/mistakes. Open to knowing more about this topic if I’ve missed out on something.

References:

1. https://stackoverflow.com/questions/4128546/advantages-of-binary-search-trees-over-hash-tables
2. http://theory.stanford.edu/~tim/s17/l/l1.pdf
3. https://medium.com/@dgryski/consistent-hashing-algorithmic-tradeoffs-ef6b8e2fcae8

Consistent hashing with bounded loads, using a Red-Black Tree was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.