What Blockchain Technologists Should Know About Voting Theory

Voting is an essential element of blockchain systems. From simple consensus to hard forks, voting mechanisms are present in every aspect of the lifecycle of a blockchain application. Consensus is a term that most blockchain technologists associate with voting dynamics. Technically, consensus algorithms are programmable representations of a not-very-well-known area of computer science known as voting theory which focuses on algorithmizing decision making. Understanding some of the principles of voting theory might help to better comprehend the plethora of consensus algorithms that we are seeing these days.

Conceptually, there are different constituents that are allowed to vote in a blockchain system depending of its protocol architecture. Miners(Bitcoin, Ethereum), master-node owners(Dash), Validators(EOS), etc. are some of the parties with voting rights in different blockchain systems. The types of decisions entrusted on those parties is highly dependent on the nature of the underlying blockchain.

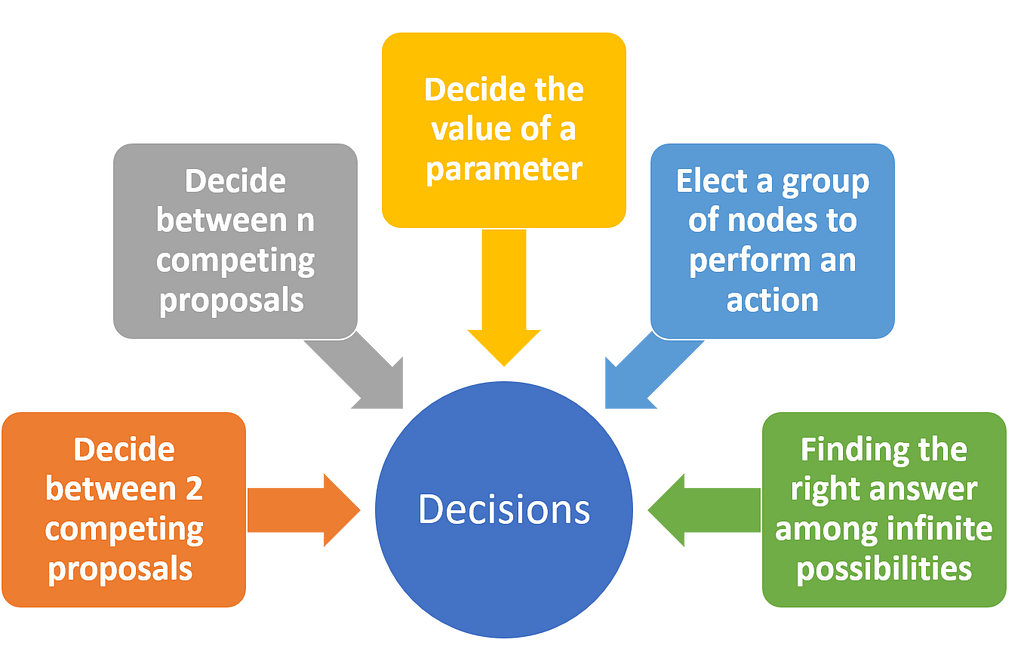
In the blockchain world voting is present everywhere. Low-level protocols such as proof-of-work(PoW) need to decide the validity of a transaction while new trends like security tokens are concerned with higher-level voting dynamics to influence the underlying assets of a crypto-security. The votes in a blockchain system can have very diverse objectives from the production of money(minting) to changes in the consensus protocol itself. Fundamentally, voting decisions in blockchain consensus can be grouped in the following categories:

· Decide between 2 competing proposals: Do we want to extend the size of the Bitcoin block or not?

· Decide between n competing proposals: The Tezos model in which you can have n possible code changes that can be implemented for a specific problem.

· Decide the value of a parameter: How many tokens to issue in an token offering?

· Elect a group of nodes to perform an action: The DFINITY model to delegate voting onto a specific set of nodes.

· Finding the right answer among infinite possibilities: What should be the size of a Bitcoin block? What should be the value of this token?

In principle, a general purpose blockchain system should be able to provide a mechanism for solving all of those types of decisions.

Voting Theory

Voting theory is the area of computer science that provides the foundation for designing voting systems. There are two desired properties that should be present in any voting model:

1. Robust to Candidates: The voting result is not affected by candidates entering or leaving the race (unless they win).
2. Robust to Voters: The voters are not rewarded for exaggerating their vote.

There are different voting methods that have evolved over the years attempting to preserve those two properties. To illustrate some of those voting methods lets imagine a scenario in which voters represented by a vector V (v1,v2, …vn) need to decide among candidates/options represented by C (c1,c2,…cm). A voting rule r will take as input a vector of votes produced by the voters and produced either a winner or an aggregate ranking of the candidate/options: r({V}) →{C}. If we extrapolate this to the blockchain world, the nature of the consensus algorithm is determined by the characteristics of the voting rule. There are different voting rule methods that have been implemented everywhere from computer systems to democratic elections.

· Plurality Vote: Each voter selects one candidate (or none if voters can abstain), and the candidate(s) with the most votes win.

· Instant Run-Off: Start with a plurality vote to determine the top two candidates (or more if there are ties). Then, there is a runoff between these candidates, and the candidate with the most votes wins.

· Anti-Plurality: Each voter votes against a single candidate, and the candidate with the fewest votes against wins

· Borda-Count: Each voter provides a linear ordering of the candidates. Each candidate is assigned a score (the Borda score) as follows: If there are n candidates, give n−1 points to candidates ranked first, n−2 points to candidates ranked second,… 1 point to a candidate ranked 2nd to last and 0. The candidate with the highest Borda score wins.

· Coombs Vote: Each voter submits a linear ordering over the set of candidates. Candidates who are ranked last by the most voters are iteratively removed. The last candidate(s) to be removed are the winner(s).

· Negative Voting: Each voter is allowed to choose one candidate to either vote for (giving the candidate one point) or to vote against (giving the candidate –1 points). The winner(s) is(are) the candidate(s) with the highest score(s) (i.e., the most positive votes).

· Approval Voting: Each voter selects a subset of the candidates (where the empty set means the voter abstains) and the candidate(s) with the most votes wins.

· Cumulative Voting: Each voter is asked to distribute a fixed number of points, say ten, among the candidates in any way they please. The candidate(s) with the most points wins the election.

· Hare Voting: The candidates/options are ordered linearly. The process repeatedly delete the candidate or candidates that receive the fewest first-place votes, with the remaining candidate(s) declared the winner (or winners in the case of ties).

Voting Paradoxes

Voting theory is full of interesting paradoxes that need to be accounted for on any implementation. Arguably, the two most famous paradoxes are the Condorcet Paradox and the Failure of Monotonicity.

Condorcet Paradox

The was first postulated by the famous Marquis de Condorcet a French philosopher and mathematician who played a primary role in the drafting of the Bourbon Constitution after the French revolution. Unfortunately, Condorcet entered in some discrepancies with the powerful Montagnards group and was labeled as a traitor, arrested and later found dead in his prison cell.

The Condorcet Paradox simply states that voting preferences in a system can be acyclical instead of transitive. If we have 3 candidates: A, B, C. We intuitive assume that voting is transitive:

If A > B and B > C then A > C

However, we can have situations in which the voting allows for cycles:

A > B and B > C and C > A

In those cases, we can’t qualitatively select the winner in an election as for each possible winner there is another candidate which voters prefer(we can select a winner quantitatively).

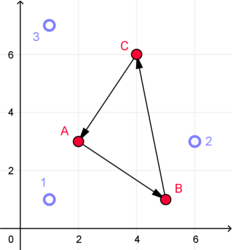Voters (blue) and candidates (red) plotted in a 2-dimensional preference space. Arrows show the order in which voters prefer the candidates.Failure of Monotonicity

A voting procedure is monotonic provided that moving up in the rankings does not adversely affect a candidate’s chances to win an election. This property captures the intuition that receiving more support from the voters is always better for a candidate. Plurality vote is the best-known example of monotonic vote: The more votes a candidate receives, the better chance the candidate has to win. Surprisingly, there are voting methods that do not satisfy this natural property. The most well-known example is plurality with runoff.

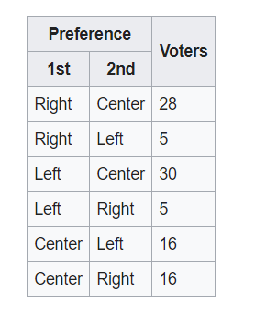
Let’s use a classic example to illustrate this paradox. Suppose the votes are cast as follows:

According to the 1st preferences, Left finishes first with 35 votes, Right gets 33 votes, and Center 32 votes, thus all candidates lack an absolute majority of first preferences. In an actual runoff between the top two candidates, Left would win against Right with 30+5+16=51 votes.

But if at least two of the five voters who ranked Right first, and Left second, would raise Left, and vote 1st Left, 2nd Right; then Left would be defeated by these votes in favor of Center. Let’s assume that two voters change their preferences in that way, which changes two rows of the table:

Now Left gets 37 first preferences, Right only 31 first preferences, and Center still 32 first preferences, and there is again no candidate with an absolute majority of first preferences. But now Right gets eliminated, and Center remains in round 2 of IRV (or the actual runoff in the Two-round system). And Center beats its opponent Left with a remarkable majority of 60 to 40 votes.

Voting Theory and Blockchains

Voting Theory is the theoretical foundation of most well-known consensus protocols. Voting is also a key element to new governance models in blockchain solutions. New areas of the crypto-asset space such as security tokens likely to push the boundaries of voting theory and find new and innovative ways as they incorporate on-chain and off-chain voting into a consistent model. Exciting times…

What Blockchain Technologists Should Know About Voting Theory was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.