Bluetooth Hacking: Cheating in Elliptic Curve Billiards

Recently, Israeli researchers from the Technion published a paper about a smart attack on vulnerable Bluetooth devices’ pairing process. This vulnerability allows attackers to bypass Bluetooth security measures and be a Man-in-the-Middle (MITM) to eavesdrop or even change the contents of a Bluetooth connection. The root cause of this vulnerability is a flawed implementation of the Elliptic Curve Cryptography within these devices.

As it often does, understanding this vulnerability is a perfect opportunity to learn how stuff really works. Therefore, this post does not stop in explaining the Bluetooth vulnerability but also provides a human-friendly explanation of the core principals of Elliptic Curve Cryptography (ECC) which is in the heart of many relevant technologies, including the SSL/TLS protocol that protects our Internet communications and ECDSA signatures that protect Bitcoin and Ethereum transactions against modifications.

Elliptic Curve Cryptography as a Billiards Game

Following Cloudflare’s Nick Sullivan blog’s terminology, Elliptic Curve Cryptography (ECC) can be described as a bizzaro Billiards game.

The Elliptic Curve, described with the equation y² = x³+ ax + b is our Billiards table.

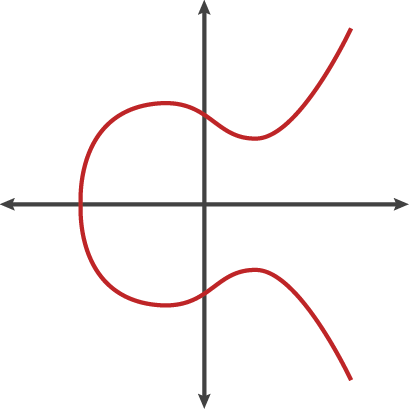A Schematic Elliptic Curve Plot (credit: CloudFlare)

Adding two points on the curve, A and B, is our Billiards shot. To add A and B, place the ball at point A and shoot it towards point B. When it hits the curve, the ball bounces either straight up (if it’s below the x-axis) or straight down (if it’s above the x-axis) to the other side of the curve and this is the result C.

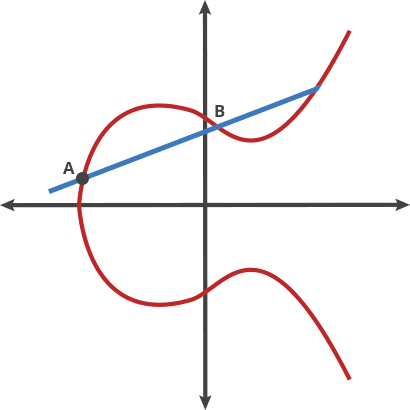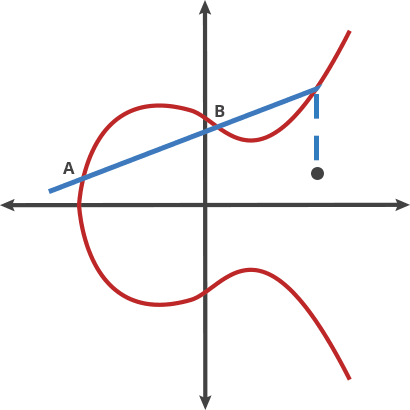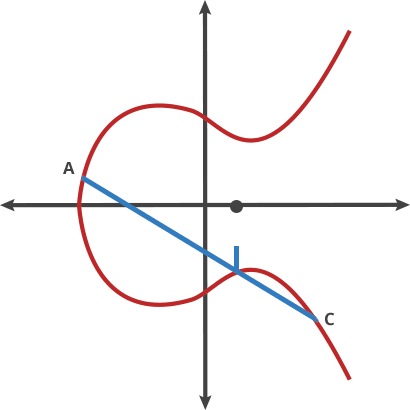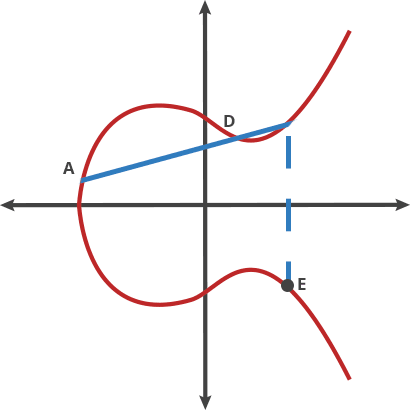Adding Two Points. A+B = C, C+A=D, A+D=E (credit: CloudFlare)

But what happens when you want to “double” a point, i.e. add a Point to itself (A+A). How can you shoot a ball from A towards A itself?

To do so, let’s choose point A’ very close to A and shot towards it. As we bring A’ closer and closer to A, the connecting line between them gets closer to the Tangent of A.

Doubling the Point P on Curve E: Shooting in the Tangent’s direction (Credit: SlideShare)

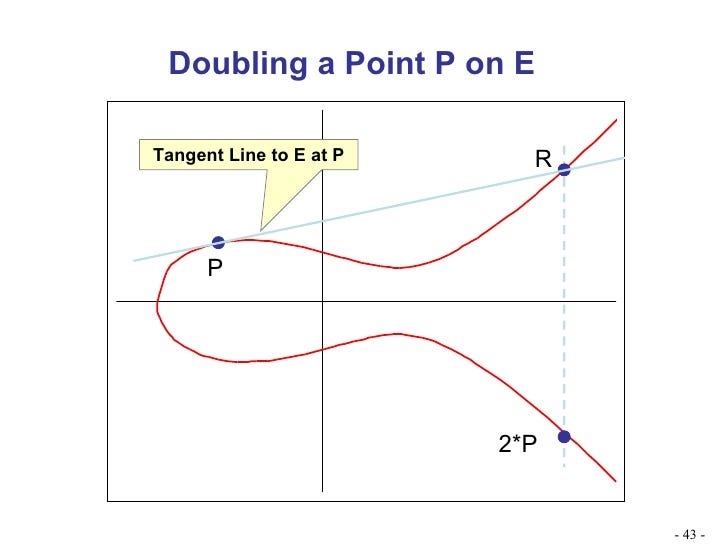
Now that we learned the basic moves let’s define the rules of the game. The player plays alone in the room. The game begins when the ball is placed on a known point P, and the player can arbitrarily choose how many times to successively shoot towards the same Point P. When the player is done, another person enters the room and tries to guess how many time the ball was struck. It turns out that the only way for him to discover that is by replaying the game shot after shot, until the table reaches the same state. However, the original player that knows in advance the number of times he intends to strike, can efficiently know the final state of the board without actually taking all these shots. Therefore this game achieves the desired cryptography “trapdoor” property: Easy to do, hard to undo.

In a more mathematical terms, calculating n*P over Elliptic Curves is easy. However, given n*P and P it’s hard to determine n.

Elliptic-Curve Diffie-Hellman: Doubles Billiard

The Elliptic-Curve Diffie-Hellman (ECDH) algorithm extends this concept further and uses the hardness of “undoing” the number of times the ball was struck in order to create a shared secret between two parties (Alice & Bob) in the presence of an Eavesdropper (Eve)

Alice, Bob and Eve (Credit: etutorials)

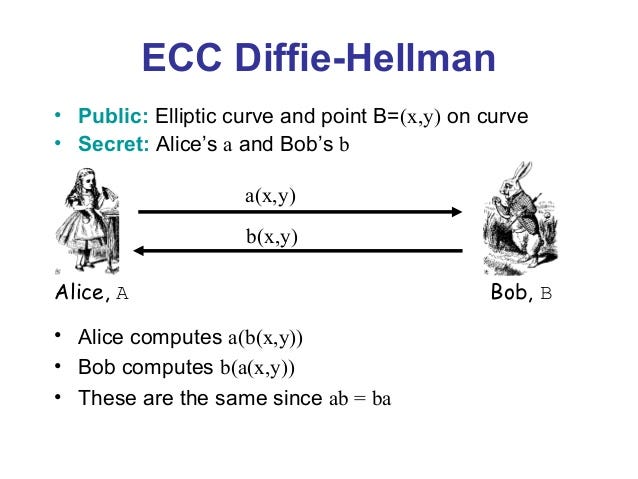
In this game of doubles, Alice plays our Billiards game alone in a room. She starts by placing the ball in a known point P and striking S₁ times (S₁*P) of her choosing. When Alice is done, she sends a photo of the table to Bob. Bob places the ball on the same place on his table (S₁*P) according to the picture and then strikes S₂ times (S₂*(S₁*P)). At the same time, Bob starts a new game on another table and strikes S₂ times (S₂*P), sending a picture to Alice so she can strike S₁ times. (S₁*(S₂*P))

By doing so, Alice and Bob individually arrived to the same final table position (S₁*S₂*P =S₂*S₁*P). They can now use the X coordinate of this final point as their shared secret.

In a more formal notation: S₁,S₂ are called secret keys, while S₁*P,S₂*P are called public keys and denoted as Pb₁ and Pb₂.

In this process neither Alice nor Bob learned about the other party’s individual secret. More importantly, Eve didn’t learn about S₁, S₂ or the final table position and the resulting shared secret, although she had access to the table pictures exchanged in the middle of the game. The pictures do tell the state of the table in the middle of the game, but revealing S₁ or S₂ is impossible, as we recall that “undoing” the number of times the ball was struck is hard.

ECC Diffie-Hellman (credit: Slideshare)

Eve strikes back!

But Eve is not done yet! Although she cannot get the shared secret by merely eavesdropping, she can actively mess with pictures sent by Alice and Bob to create wrong computations that would hopefully help her in obtaining the shared secret.

Bluetooth designers were aware of that risk. When two Bluetooth devices are pairing (i.e. connect to each other) they use ECDH to create a shared secret to be used later to protect the secrecy and integrity of the communication. To protect against an active Man-in-the-Middle that can fiddle with ECDH messages, an extra layer of protection was added to verify that the X coordinates of the sent public keys points (the “pictures” in our analogy) were not changed by an attacker.

However, the Bluetooth protocol doesn’t mandates the verification of the Y coordinates. That’s exactly the gap the researchers were able to abuse in order to completely break the security of the Bluetooth pairing process.

The way Eve can abuse this fact is by changing the pictures of the table and placing the ball (public key) in a very special place on another shape of the table (another curve). In mathematical terms, Eve is zeroing the Y coordinate of the public keys exchanged by Alice and Bob. Since the Y coordinates are not verified by the protocol Eve can get away with cheating about them.

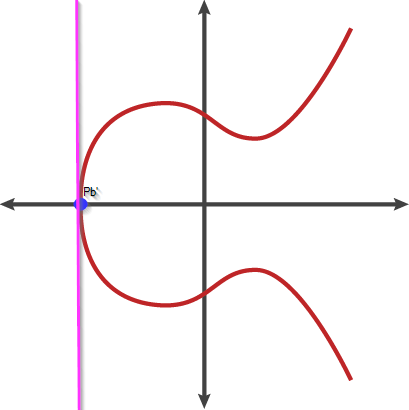The fiddled Public Key (Pb’) is placed on the X axis. Its tangent is a straight line

This point of the curve has a very interesting property. Usually when we play our game of repeatedly shooting the ball towards the same point, the ball hits the curve in all kinds of angles and changes its position with each shot without returning to the same point. However, when we place the ball on the X axis and shoot it towards that point repeatedly the game is very dull. As you recall doubling a point is shooting in the direction of the tangent, which is a straight line (see figure above). This line actually never intersects with the curve and therefore the ball needs to be “artificially” stopped on a point named “point-at-infinity” or ∞. On the next shot, the ball is shot towards the original point and ends there. The next shots merely repeat that process. On every even addition the ball reaches ∞, on every odd addition the ball lands back on the X axis. It’s like shooting the billiards ball on a right angle: since it doesn’t hit the curve with an angle, it can only bounce from the table edge on a right angle again in a very predictable and boring way.

But boring and predictable is exactly what Eve wants! She replaces the original pictures (Pb₁, Pb₂) of the table with pictures of “fixed-up” tables (Pb₁', Pb₂'). If both S₁,S₂ happen to be even then the result will be S₂*Pb₁' = ∞ =S₁*Pb₂'. As a result, the pairing will be successful and will create a shared key that Eve knows! In any other case, i.e. if either s1 or s2 is odd the pairing will fail as Pb₁’≠ Pb₂’≠∞.

Therefore, Eve has 25% success rate in finding the shared secret that allows her to eavesdrop and manipulate Bluetooth traffic. 25% may sound low, but since victim users are very likely to retry to pair if pairing has failed, then eventually Eve will be successful. And since the Y coordinates are not validated throughout the rest of the protocol, Eve’s cheating is not exposed.

( The researchers detail a more sophisticated attack that has 50% success rate, but that’s a matter for another post)

Final thoughts

Implementing cryptography is hard and even subtle mistakes might get heavily punished. Implementations need to be scrutinized to make sure they are indeed adhere to best practices. That is the main reason for us in KZen Networks to open source our cryptography algorithms implementations.

KZen networks

On the other hand, understanding attacks against implementation can help builders gain better understanding of not only about correct implementation, but also of how stuff actually works.

Enjoy your ECC Billiards!

Bluetooth Hacking: Cheating in Elliptic Curve Billiards was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.