Linear Regression in 2 Minutes (using PyTorch)

This is Part 2 of the PyTorch Primer Series.

Linear Regression is linear approach for modeling the relationship between inputs and the predictions

Source: Wikipedia

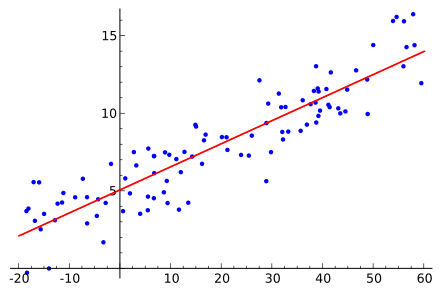
We find a ‘Linear fit’ to the data.

Fit: We are trying to predict a variable y, by fitting a curve (line here) to the data. The curve in linear regression follows a linear relationship between the scalar (x) and dependent variable.

Creating Models in PyTorch

1. Create a Class
2. Declare your Forward Pass
3. Tune the HyperParameters

class LinearRegressionModel(nn.Module):def __init__(self, input_dim, output_dim):        super(LinearRegressionModel, self).__init__() # Calling Super Class's constructor        self.linear = nn.Linear(input_dim, output_dim)# nn.linear is defined in nn.Moduledef forward(self, x):# Here the forward pass is simply a linear function        out = self.linear(x)return outinput_dim = 1output_dim = 1

Steps

1. Create instance of model
2. Select Loss Criterion
3. Choose Hyper Parameters

model = LinearRegressionModel(input_dim,output_dim)criterion = nn.MSELoss()# Mean Squared Lossl_rate = 0.01optimiser = torch.optim.SGD(model.parameters(), lr = l_rate) #Stochastic Gradient Descentepochs = 2000

Training The Model

for epoch in range(epochs):    epoch +=1    #increase the number of epochs by 1 every time

    inputs = Variable(torch.from_numpy(x_train))    labels = Variable(torch.from_numpy(y_correct))#clear grads as discussed in prev post

    optimiser.zero_grad()

    #forward to get predicted values

    outputs = model.forward(inputs)    loss = criterion(outputs, labels)    loss.backward()# back props    optimiser.step()# update the parameters    print('epoch {}, loss {}'.format(epoch,loss.data[0]))

Finally, Print the Predicted Values

predicted =model.forward(Variable(torch.from_numpy(x_train))).data.numpy()plt.plot(x_train, y_correct, 'go', label = 'from data', alpha = .5)plt.plot(x_train, predicted, label = 'prediction', alpha = 0.5)plt.legend()plt.show()print(model.state_dict())

If you want to read about Week 2 in my Self Driving Journey, here is the blog post

The Next Part in the Series will discuss about Linear Regression.

You can find me on Twitter @bhutanisanyam1, connect with me on Linkedin hereSubscribe to my Newsletter for a weekly curated list of Deep Learning and Computer Vision Reads

Linear Regression in 2 Minutes (using PyTorch) was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.